Sarah Hammond
This project began as a desire to create a Gödel Escher Bach-inspired « strange loop. » In this cult-classic tome, the author, Douglas Hofstadter, flits between math, art, and music to weave a complicated theorem about his self-defined « strange loops, » slightly paradoxical infinite loops that end where they began. Some of the most famous examples he cites include the Mobius strip and the Penrose stairs, though strange loops are not limited to geometric paradoxes.
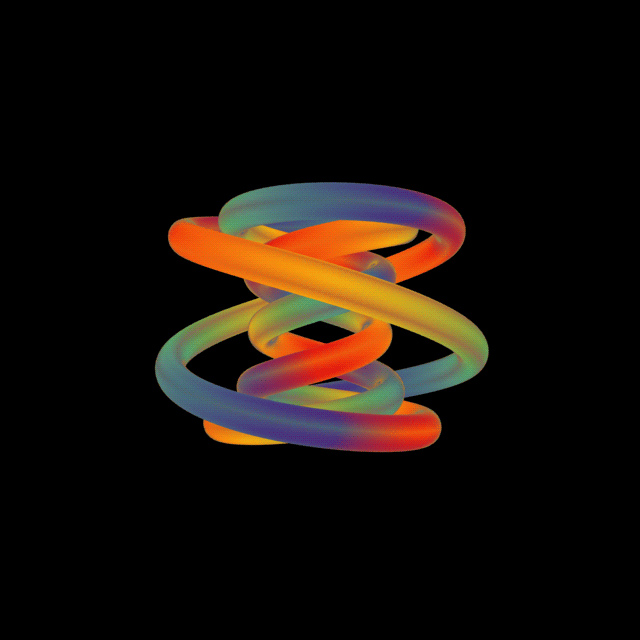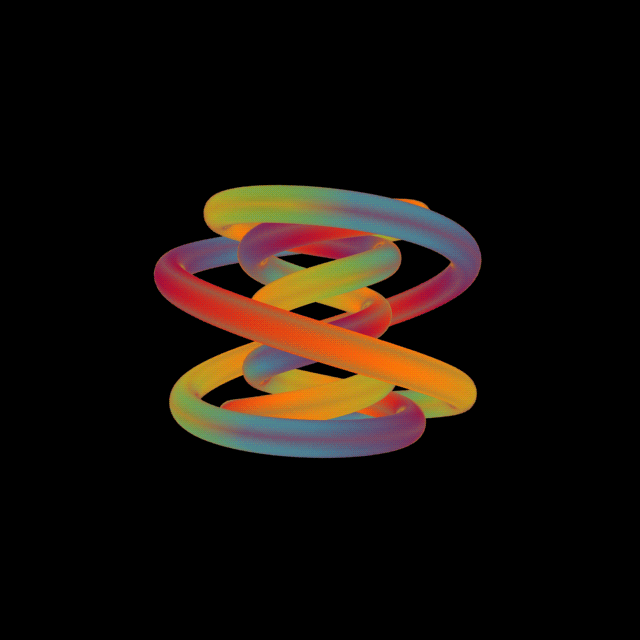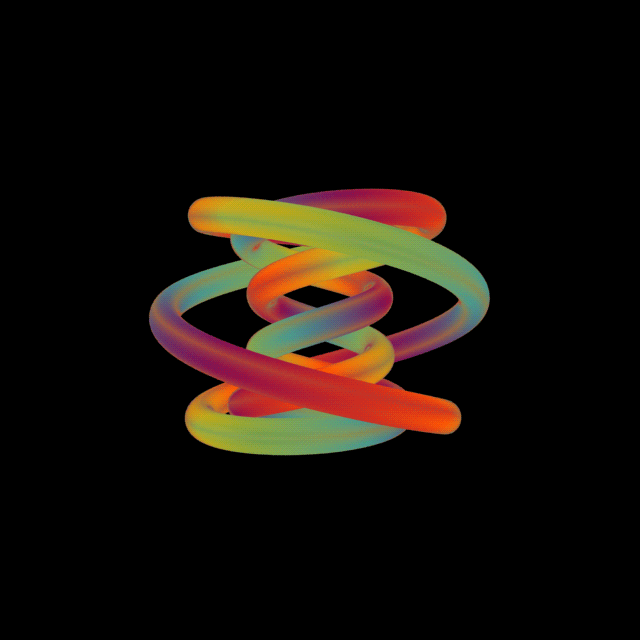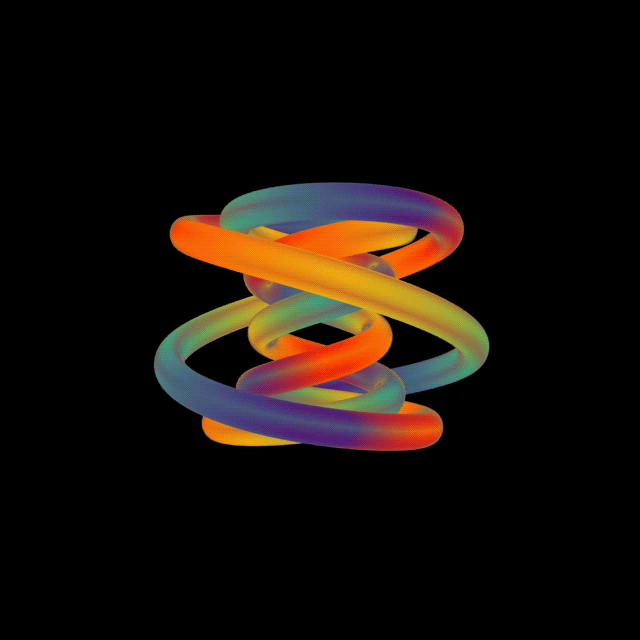
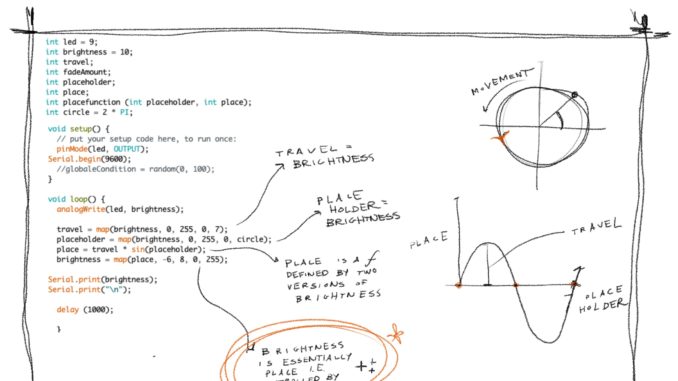
The goal of this project was to illustrate a degree of infinite strangeness within the ultimately ordered and logical universe of C++, or more precisely the Arduino IDO. The physical proof would only be a single output LED, poised to illustrate this loop visually.
Logically capturing illogic did prove insanely complex, though the difficulty tended to be in maintaining clarity of mission and argument. I created a few different working models that each illustrate a particular component of illogic, albeit imperfectly. For each of these models, I tried at least four other logical arguments that proved truly paradoxical and impossible.
I do have to admit, in submitting these exercises, that I haven’t found a model I’m completely happy with in terms of its truth of comparison and/or logical conclusion. However, I can say I’m currently teetering on obsession and plan to continue trying.
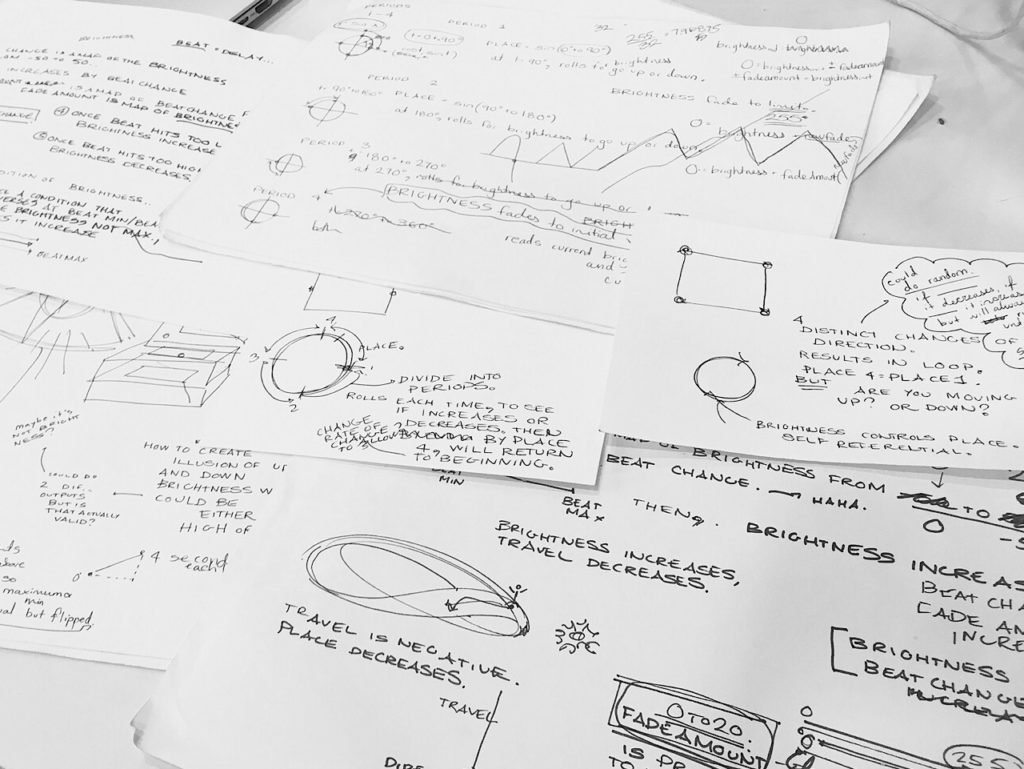
The First Attempt:
Self Referential Circle
This exercise centers about a self-referential loop created with geometry of sine functions. Logically, self-reference adds an element of strangeness that nods to Hofstader’s loops, though remains possible here through the use of map functions. Metaphorically, this adds a bit of twist to the loop as it continues and feeds into itself.
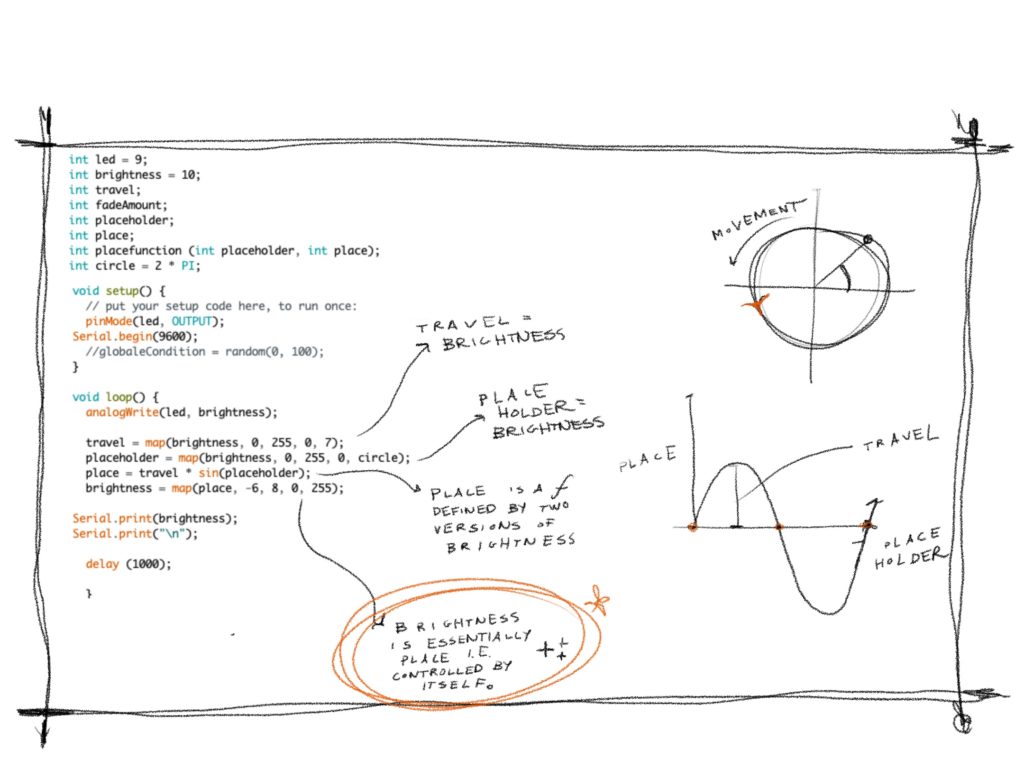
This loop was successful in generating looped and continuous incremental values, despite the slight self-definition, which can easily fall into paradox in the logical realm of Arduino.
The Second Attempt:
Randomized Penrose Stair
This attempt was more focused upon the geometry of Eschers’ stairs, hoping to embody some level of this geometry in the world of Arduino code. The Penrose stairs specifically have four distinct points of change, while circling continuously. To represent this, I created a measurement representative of the position on the loop, divided into four periods. One’s initial position is randomized, and from there one travels in increments either up or down the stairs, an analog for each geometric stair. The direction of travel is randomized, while the increments remain in tact, but the loop is never broken. If chance allows, the initial position is passed and recovered.

It’s possible to recover the initial position mostly due to the distinct increments of change. It’s also important to note that at each moment of change, generated randomness chooses the direction of travel. With brightness as an analog for position, this differs from Escher’s stairs which do seem to always have one direction of travel. My thought was that randomness could represent illusion and flawed perception common in Escher’s drawings. However, I believe there may be a better way to represent the Penrose stairs specifically.

This project was very code-based and not focused upon user interface, which I left at its absolute essentials to direct the focus to reading and understanding the logic of the code. Once one understands this, they watch the serial monitor and the singular light to understand its effects through time.
In all, this proved to be some of the most intense, focused thinking I’ve done in a while. The logic and figuring of tens of pages of scrap paper was definitely the most rewarding part, as I’m not quite there yet with either of these models. However, I really enjoyed complicating such simple hardware (LED, board) with theoretics and the concepts of Model, Escher, Bach.